Publicaciones de Estudiantes

Autor: RITO ANTONIO MONCADA PINZON
Titulo: DINAMICA
Area:
Pais:
Perfil:
Programa:
Disponible para descarga: Yes
Ver Más Publicaciones Estudiantiles Clic aquí
Diseminar información, ideas innovadoras y conocimientos académicos es una función importante para Atlantic Internacional University. Publicaremos noticias, artículos, comentarios y otras publicaciones de nuestros estudiantes y otros colaboradores. Si desea contactar al autor por motivos profesionales favor enviar su petición por este medio.
Para conocer más de la iniciativa de Acceso Abierto de AIU haga Clic aquí.
INTRODUCCIÓN
El estar involucrado en proyectos complejos, donde se tocan temas muy variados, mecánica de materiales, mecánica
de fluidos, electricidad, instrumentación etc., es muy importante conocer las teorías físicas de porque se hacen y no se
hacen los proyectos, de donde se sacan los conceptos definitivos del porque funciona un oleoducto, una bomba etc.,
eso me inquieto a conocer este tema que es tan relevante en el desarrollo de la vida cotidiana, nada se mueve,
nada funciona sin un principio lógico dentro de la física y por supuesto dentro de la dinámica.
Este tema están extenso e interesante que podríamos escribir miles de páginas mostrando lógicas y ejemplos y
nunca finalizaríamos.
En esta exposición trato los temas y principios básicos de la dinámica:
La Dinámica es la parte de la física que describe la evolución en el tiempo de un sistema físico en relación a las causas que provocan los cambios de estado físico y/o estado de movimiento. El objetivo de la dinámica es describir los factores capaces de producir alteraciones de un sistema físico, cuantificarlos y plantear ecuaciones de movimiento o ecuaciones de evolución para dicho sistema.
El estudio de la dinámica es prominente en los sistemas mecánicos (clásicos, relativistas o cuánticos), pero también la termodinámica y electrodinámica. En este artículo se desarrollaran los aspectos principales de la dinámica en sistemas
mecánicos, dejándose para otros artículos el estudio de la dinámica en sistemas no-mecánicos.
El fenómeno más obvio y fundamental que observamos a nuestro alrededor es el de movimiento. El viento, las olas, los pájaros que vuelan, los animales que corren, las hojas que caen. Prácticamente todos los procesos inimaginables pueden describirse como el movimiento de ciertos objetos. Para analizar y predecir la naturaleza de los movimientos que resultan de las diferentes clases de interacciones, se han inventado algunos conceptos importantes tales como los de momentum, fuerza y energía. Si el momentum, la fuerza, y la energía se conocen y se expresan en un modo cuantitativo es posible establecer reglas mediante las cuales pueden predecirse los movimientos resultantes.
La mecánica, es la ciencia del movimiento, es también la ciencia del momentum, la fuerza y la energía; de ella se derivan: la cinemática, que estudia el movimiento sin tomar en consideración las fuerzas que lo producen, y la dinámica, que a diferencia de la cinemática, fundamenta el estudio del movimiento en las leyes del movimiento propuestas por Newton.
Las leyes de Newton para el movimiento de los cuerpos han sido formuladas de una gran variedad de formas. Para nuestro propósito, las expresamos como sigue:
* Una partícula bajo el efecto de un sistema de fuerzas equilibradas tiene aceleración nula.
* Una partícula bajo el efecto de un sistema de fuerzas no equilibradas tiene una aceleración directamente proporcional a la resultante del sistema de fuerzas y paralela a ella.
* Las fuerzas de acción y de reacción entre dos partículas son siempre iguales y de direcciones contrarias.
Peso de un cuerpo. El peso de un cuerpo es la fuerza de atracción gravitacional ejercida sobre el cuerpo por la Tierra y depende de su posición respecto al centro de la Tierra.
Masa de un cuerpo. La masa M de un cuerpo es la cantidad de materia que contiene y es independiente del lugar donde se encuentre; también se le conoce como masa inercial ya que representa la inercia de un cuerpo, es decir la resistencia de un cuerpo al cambio en su movimiento.
A la razón entre el peso P de un cuerpo y la constante gravitacional g: , se le conoce como masa gravitacional M. Pero como el peso y la constante gravitacional varían de acuerdo a su posición con respecto al centro de la Tierra, no se ha podido demostrar ninguna diferencia entre la masa gravitacional y la masa inercial, por lo que se tomarán indistintamente.
Partícula. El término partícula suele referirse a un objeto cuyo tamaño se reduce a un punto.
Cuerpo. El termino cuerpo suele referirse a un sistema de partículas que forman un objeto de tamaño apreciable. Sin embargo el criterio del tamaño es relativo, por lo cual los términos cuerpo y partícula se pueden aplicar al mismo objeto si es que la masa no se toma en cuenta en el análisis.
SISTEMAS DE UNIDADES
| Sistema |
Longitud |
Tiempo |
Fuerza |
Masa |
| Gravitacional Inglés |
pie (pie) |
segundo
(seg, s) |
libra fuerza,
lb, pound |
slug
 |
| Gravitacional Métrico técnico. |
metro (m) |
Seg |
kilogramo fuerza (kgf) |
utm
 |
| Métrico absoluto CGS |
centímetro (cm) |
Seg |
dina
 |
gramo
gr |
| Métrico absoluto MKS |
metro (m) |
Seg |
newton
 |
kilogramo
kg |
CONTENIDOS
· Movimiento uniforme acelerado y no acelerado.
· Características cinemáticas de cuerpos en caída libre.
· Características cinemáticas de cuerpos en movimiento parabólico.
· Características cinemáticas de cuerpos en movimiento circular.
· Leyes del movimiento de Newton.
· Fuerzas de rozamiento: estático y dinámico.
· Cinemática vectorial: vector posición, vector velocidad y vector aceleración.
· Cinemática vectorial: radio de curvatura en movimientos circulares.
CONOCIMIENTOS PREVIOS
· Multiplicación de vectores: escalar y vectorial.
· Álgebra matricial: matriz adjunta y teorema del cofactor.
· Cálculo infinitesimal: límite y derivación de funciones matemáticas.
· Cálculo integral: integrales definidas con límites de integración.
· Trigonometría plana.
· Descomposición rectangular de vectores: Diagrama de Cuerpo Libre (DCL).
VELOCIDAD Y ACELERACION:
Ecuaciones básicas.
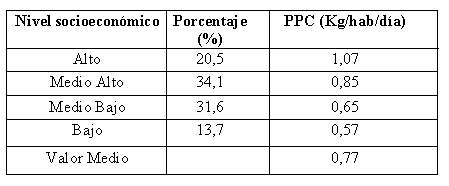
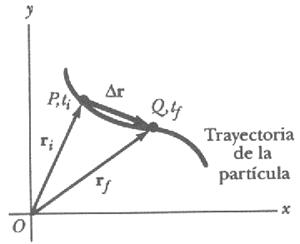
La velocidad media de una partícula durante un intervalo de tiempo t, está definida como la razón entre el desplazamiento y el intervalo de tiempo (Figura 1).
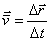
(1)
Donde:
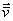
: Velocidad media del móvil, m/s
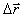
: Magnitud del desplazamiento del móvil, m
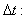
:Intervalo de tiempo, s
Como el desplazamiento es una cantidad vectorial y el intervalo de tiempo es una cantidad escalar, concluimos que la velocidad promedio es una cantidad vectorial dirigida a lo largo de
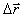
.
Figura 1.
Una partícula que se mueve en el plano x-y se localiza a través del vector posición dibujado desde el origen del sistema referencial inercial. El desplazamiento de la partícula cuando se mueve de P a Q en el intervalo

= tf - ti, es igual al vector =
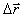
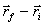
.
Un concepto derivado de la velocidad media, es la velocidad instantánea, la cual se define como el límite de la velocidad promedio,
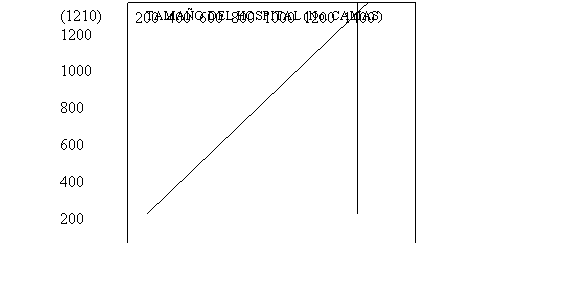
, conforme

tiende a cero.
(2)
La velocidad instantánea es igual a la derivada del vector de posición respecto del tiempo. La dirección del vector velocidad instantánea en cualquier punto en una trayectoria de la partícula está a lo largo de la línea que es tangente a la trayectoria en ese punto y en la dirección del movimiento. A la magnitud del vector de velocidad instantánea recibe el nombre de “rapidez”.
La velocidad media al igual que la velocidad instantánea se expresa m/s en el sistema internacional; Ft/s en el sistema británico (se lee pies por segundo), y cm/s en el sistema c.g.s.
Dado que la velocidad de un móvil puede variar en el tiempo, nació un concepto denominado aceleración, la cual se define como la razón de cambio del vector velocidad,

, en un tiempo transcurrido

.
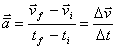
(3)
Donde:
Vf: velocidad final del movimiento, m/s
Vi: velocidad inicial del movimiento, m/s
tf – ti: intervalo de tiempo trascurrido para que el móvil pase de Vi a Vf.
Puesto que la aceleración promedio es la razón entre una cantidad vectorial,

, y una cantidad escalar,

, se concluye que,

, es una cantidad vectorial dirigida a lo largo de

.
Un concepto derivado de la aceleración promedio, es la aceleración instantánea, la cual se define como el valor límite de la razón

, cuando,

, tiende a cero.
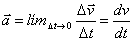
(4)
En otras palabras, la aceleración instantánea es igual a la razón de cambio del vector velocidad respecto al tiempo.
Es importante tener en cuenta tres situaciones donde un móvil tiene una aceleración asociada: cuando la magnitud del vector (la rapidez) cambia con el tiempo; como en un movimiento acelerado en línea recta; cuando sólo la dirección del vector velocidad cambia con el tiempo sin que su magnitud varíe, como en un movimiento curvilíneo; y por último, cuando tanto la magnitud como la dirección del vector velocidad se modifican continuamente.
La aceleración media, así como la aceleración instantánea se expresan en m/s2 en el sistema internacional, en Ft/s2 en el sistema británico (se lee pies por segundo cuadrado), y cm/s2 en el sistema c.g.s.
El hecho de que un cuerpo se desplace con una aceleración de 15 m/s2, implica que cada segundo su velocidad aumenta 15 m/s. También pudiese darse el caso de que un móvil ostente una aceleración negativa, por ejemplo de – 8 m/s2, lo cual indica que cada segundo su velocidad decae 8 m/s. Por último, si un móvil tiene una aceleración igual a cero, puede inferirse que: posee una velocidad constante, o se encuentra en reposo.
DINAMICA DE FLUIDOS
Fluidos: Se denomina así al sistema de partículas que a diferencia de los sólidos, no están unidas rígidamente y pueden moverse con una cierta libertad unas respecto de las otras.
Esto le permite ceder a cualquier fuerza tendiente a alterar su forma, con lo que fluye adaptándose a la del recipiente.
Esta designación engloba a la materia que se encuentra en los estados líquido y gaseoso.
La diferencia entre el fluido líquido y el gaseoso radica en que las partículas que componen un líquido se encuentran más unidas que las de un gas; por esta razón, el volumen del líquido dentro de un recipiente, permanece constante con una superficie límite bien definida, mientras que el del gas no posee límite y se difunde en el aire disminuyendo su densidad.
Fluidos ideales
La dinámica de fluidos trata del estudio de los fluidos en movimiento y constituye una de las ramas más complicadas de la mecánica, como puede comprobarse
considerando ejemplos tan corrientes de movimiento de fluidos como un río desbordado o los remolinos del humo de un cigarro. Aunque sigue cumpliéndose la ecuación F = ma en todo instante para cada gota de agua y cada partícula de humo, puede imaginarse la complicación que resultaría si tuviéramos que escribir las ecuaciones de movimiento de cada partícula. Sin embargo, el problema no es tan insoluble como parece a primera vista.
Cuando se cumplen condiciones adecuadas, el movimiento de un fluido corresponde a un tipo relativamente sencillo, llamado currentilineo o estacionario. a figura 1 representa una porción de un tubo el cual un fluido se mueve de izquierda a derecha. Si el movimiento es de tipo estacionario, cada partícula que pasa por un punto tal como el a sigue exactamente la misma trayectoria que las partículas precedentes que pasaron por dicho punto. Estas trayectorias se llaman líneas de flujo o líneas de corriente, y en la figura se han representado tres de ellas.
Si la sección transversal del tubo varía un punto a otro, la velocidad de cada partícula variará a lo largo de su línea de corriente; pero, en cualquier punto fijo del tubo, la de la partícula que pase por dicho punto es siempre la misma.
Fluido Ideal:
* 1.-Fluido no viscoso. Se desprecia la fricción interna entre las distintas partes del fluido
* 2.-Flujo estacionario. La velocidad del fluido en un punto es constante con el tiempo
* 3.-Fluido incompresible. La densidad del fluido permanece constante con el tiempo
* 4.-Flujo irrotacional. No presenta torbellinos, es decir, no hay momento angular del fluido respecto de cualquier punto.
Ecuación de la continuidad
La ecuación de continuidad o conservación de masa es una herramienta muy útil para el análisis de fluidos que fluyen a través de tubos o ductos con diámetro variable. En estos casos, la velocidad del flujo cambia debido a que el área transversal varía de una sección del ducto a otra.
La figura representa un tubo por el cual circula un fluido de izquierda a derecha. Sea S1 el área de la sección transversal en el punto (1) y v1 la velocidad. Durante el tiempo t, las partículas del fluido que se encuentran inicialmente en (1) avanzarán una distancia v1t y atravesará la sección S1 un volumen de fluido igual a S1v1t. El volumen de fluido que atraviesa por unidad de tiempo es, por tanto, igual a S1 v1. Análogamente, el volumen de fluido que atravesará por unidad de
BIBLIOGRAFIA
Alonso, M. y Finn, E. (1986) Física. Volumen I: Mecánica. Addison – Wesley Iberoamericana.
Resnick, R. y Halliday, D. (1984) Física. Tomo I (séptima impresión). Compañía Editorial Continental: México.
Serway, Raymond (1998) Física. Tomo I (Cuarta edición). Mc Graw-Hill: México.
Mecánica vectorial para ingeniería - dinámica. F.P. Beer y E.R. Johnston - Ed.
McGraw-Hill.
Mecánica para ingenieros - dinámica. T.C. HUang - Ed. Fondo Educativo Int. S.A.
Problemas de mecánica. A.Giet - Ed. Marcombo

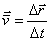 (1)
(1)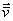 : Velocidad media del móvil, m/s
: Velocidad media del móvil, m/s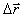 : Magnitud del desplazamiento del móvil, m
: Magnitud del desplazamiento del móvil, m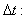 :Intervalo de tiempo, s
:Intervalo de tiempo, s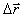 .
.
 = tf - ti, es igual al vector =
= tf - ti, es igual al vector = 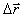
 (2)
(2)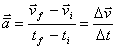 (3)
(3)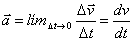 (4)
(4)