Author: Fawad Iftikhar Butt
Title: Statistical Thinking for Decision Making
Area: Business Administration
Country:
Program: Doctorate
Available for Download: Yes
View More Student Publications Click here

Sharing knowledge is a vital component in the growth and advancement of our society in a sustainable and responsible way. Through Open Access, AIU and other leading institutions through out the world are tearing down the barriers to access and use research literature. Our organization is interested in the dissemination of advances in scientific research fundamental to the proper operation of a modern society, in terms of community awareness, empowerment, health and wellness, sustainable development, economic advancement, and optimal functioning of health, education and other vital services. AIU’s mission and vision is consistent with the vision expressed in the Budapest Open Access Initiative and Berlin Declaration on Open Access to Knowledge in the Sciences and Humanities. Do you have something you would like to share, or just a question or comment for the author? If so we would be happy to hear from you, please use the contact form below.

For more information on the AIU's Open Access Initiative, click here.

Sr. No.	Name of Topic	Page No.
1	Introduction	3
2	Objectives	4
3	Statistical thinking for decision making	5
4	Statistical Modeling for Decision-Making under Uncertainties	8
5	Statistical Decision-Making Process	9
6	Understanding Business Statistics	10
7	Common Statistical Terminology with Applications	11
8	Type of Data & Sampling Methods	14
9	Statistical Summaries (Mean, Median, Mode)	16
10	Probability, Chance, Likelihood, and Odds	22
11	Estimation & Sample size determination	25
12	Regression Analysis	29
13	Index Numbers	32
14	Bibliography	35

Introduction (Purpose of Selection)
Today's good decisions are driven by data. In all aspects of our lives, and importantly in the business context, an amazing diversity of data is available for inspection and analytical insight. Business managers and professionals are increasingly required to justify decisions on the basis of data. They need statistical model-based decision support systems. Statistical skills enable them to intelligently collect, analyze and interpret data relevant to their decision-making. Statistical concepts and statistical thinking enable them to:

• solve problems in a diversity of contexts.
• add substance to decisions.
• reduce guesswork.

In competitive environment, business managers must design quality into products, and into the processes of making the products. They must facilitate a process of never-ending improvement at all stages of manufacturing and service. This is a strategy that employs statistical methods, particularly statistically designed experiments, and produces processes that provide high yield and products that seldom fail. Moreover, it facilitates development of robust products that are insensitive to changes in the environment and internal component variation. Carefully planned statistical studies remove hindrances to high quality and productivity at every stage of production. This saves time and money. It is well recognized that quality must be engineered into products as early as possible in the design process. One must know how to use carefully planned, cost-effective statistical experiments to improve, optimize and make robust products and processes.

Purpose of Selection

The purpose of the selection of this course is to obtain better understanding of Statistics as it is very important tool for modern business decisions and hence a basic necessity in any area of activity.

Objectives

• Understanding Statistics- the basis in decision making
• Functions of Operations Management:
• Statistical Modeling for Decision-Making under Uncertainties
• Statistical Decision-Making Process
• Understanding Business Statistics
• Common Statistical Terminology with Applications
• Type of Data & Sampling Methods
• Statistical Summaries (Mean, Median, Mode)
• Probability, Chance, Likelihood, and Odds
• Estimation & Sample size determination
• Regression Analysis
• Index Numbers
  

1) Statistical Thinking for Decision Making
Today's good decisions are driven by data. In all aspects of our lives, and importantly in the business context, an amazing diversity of data is available for inspection and analytical insight. Business managers and professionals are increasingly required to justify decisions on the basis of data. They need statistical model-based decision support systems. Statistical skills enable them to intelligently collect, analyze and interpret data relevant to their decision-making. Statistical concepts and statistical thinking enable them to:

• solve problems in a diversity of contexts.
• add substance to decisions.
• reduce guesswork.

In competitive environment, business managers must design quality into products, and into the processes of making the products. They must facilitate a process of never-ending improvement at all stages of manufacturing and service. This is a strategy that employs statistical methods, particularly statistically designed experiments, and produces processes that provide high yield and products that seldom fail. Moreover, it facilitates development of robust products that are insensitive to changes in the environment and internal component variation. Carefully planned statistical studies remove hindrances to high quality and productivity at every stage of production. This saves time and money. It is well recognized that quality must be engineered into products as early as possible in the design process. One must know how to use carefully planned, cost-effective statistical experiments to improve, optimize and make robust products and processes.
Business Statistics is a science assisting you to make business decisions under uncertainties based on some numerical and measurable scales. Decision making processes must be based on data, not on personal opinion nor on belief. The Devil is in the Deviations: Variation is inevitable in life! Every process, every measurement, every sample has variation. Managers need to understand variation for two key reasons. First, so that they can lead others to apply statistical thinking in day-to-day activities and secondly, to apply the concept for the purpose of continuous improvement. Therefore, remember that:
Just like weather, if you cannot control something, you should learn how to measure and analyze it, in order to predict it, effectively. If you have taken statistics before, and have a feeling of inability to grasp concepts, it may be largely due to your former non-statistician instructors teaching statistics. Their deficiencies lead students to develop phobias for the sweet science of statistics. In this respect, Professor Herman Chernoff (1996) made the following remark: "Since everybody in the world thinks he can teach statistics even though he does not know any, I shall put myself in the position of teaching biology even though I do not know any"
Inadequate statistical teaching during university education leads even after graduation, to one or a combination of the following scenarios:

1. In general, people do not like statistics and therefore they try to avoid it.
2. There is a pressure to produce scientific papers, however often confronted with "I need something quick."
3. At many institutes in the world, there are only a few (mostly 1) statisticians, if any at all. This means that these people are extremely busy. As a result, they tend to advise simple and easy to apply techniques, or they will have to do it themselves.
4. Communication between a statistician and decision-maker can be difficult. One speaks in statistical jargon; the other understands the monetary or utilitarian benefit of using the statistician's recommendations.

The Birth of Probability and Statistics
The original idea of "statistics" was the collection of information about and for the "state". The word statistics derives directly, not from any classical Greek or Latin roots, but from the Italian word for state.
The birth of statistics occurred in mid-17th century. A commoner, named John Graunt, who was a native of London, began reviewing a weekly church publication issued by the local parish clerk that listed the number of births, christenings, and deaths in each parish. These so called Bills of Mortality also listed the causes of death. Graunt who was a shopkeeper organized this data in the form we call descriptive statistics, which was published as Natural and Political Observations Made upon the Bills of Mortality. Shortly thereafter he was elected as a member of Royal Society. Thus, statistics has to borrow some concepts from sociology, such as the concept of Population. It has been argued that since statistics usually involves the study of human behavior, it cannot claim the precision of the physical sciences. Probability has much longer history. Probability is derived from the verb to probe meaning to "find out" what is not too easily accessible or understandable. The word "proof" has the same origin that provides necessary details to understand what is claimed to be true. Probability originated from the study of games of chance and gambling during the 16th century. Probability theory was a branch of mathematics studied by Blaise Pascal and Pierre de Fermat in the seventeenth century. Currently in 21st century, probabilistic modeling is used to control the flow of traffic through a highway system, a telephone interchange, or a computer processor; find the genetic makeup of individuals or populations; quality control; insurance; investment; and other sectors of business and industry.
New and ever growing diverse fields of human activities are using statistics; however, it seems that this field itself remains obscure to the public. Professor Bradley Efron expressed this fact nicely: During the 20th Century statistical thinking and methodology have become the scientific framework for literally dozens of fields including education, agriculture, economics, biology, and medicine, and with increasing influence recently on the hard sciences such as astronomy, geology, and physics. In other words, we have grown from a small obscure field into a big obscure field.

2) Statistical Modeling for Decision-Making under Uncertainties:
From Data to the Instrumental Knowledge
In this diverse world of ours, no two things are exactly the same. A statistician is interested in both the differences and the similarities; i.e., both departures and patterns.
The actuarial tables published by insurance companies reflect their statistical analysis of the average life expectancy of men and women at any given age. From these numbers, the insurance companies then calculate the appropriate premiums for a particular individual to purchase a given amount of insurance.
Data must be collected according to a well-developed plan if valid information on a conjecture is to be obtained. The plan must identify important variables related to the conjecture, and specify how they are to be measured. From the data collection plan, a statistical model can be formulated from which inferences can be drawn.
As an example of statistical modeling with managerial implications, such as "what-if" analysis, consider regression analysis. Regression analysis is a powerful technique for studying relationship between dependent variables (i.e., output, performance measure) and independent variables (i.e., inputs, factors, decision variables). Summarizing relationships among the variables by the most appropriate equation (i.e., modeling) allows us to predict or identify the most influential factors and study their impacts on the output for any changes in their current values.
Data is known to be crude information and not knowledge by itself. The sequence from data to knowledge is: from Data to Information, from Information to Facts, and finally, from Facts to Knowledge. Data becomes information, when it becomes relevant to your decision problem. Information becomes fact, when the data can support it. Facts are what the data reveals. However the decisive instrumental (i.e., applied) knowledge is expressed together with some statistical degree of confidence. Fact becomes knowledge, when it is used in the successful completion of a decision process. Considering the uncertain environment, the chance that "good decisions" are made increases with the availability of "good information." The chance that "good information" is available increases with the level of structuring the process of Knowledge Management. The above figure also illustrates the fact that as the exactness of a statistical model increases, the level of improvements in decision-making increases.

3) Statistical Decision-Making Process
Unlike the deterministic decision-making process, such as linear optimization by solving systems of equations, Parametric systems of equations and in decision making under pure uncertainty, the variables are often more numerous and more difficult to measure and control. However, the steps are the same. They are:

1. Simplification
2. Building a decision model
3. Testing the model
4. Using the model to find the solution:
• It is a simplified representation of the actual situation
• It need not be complete or exact in all respects
• It concentrates on the most essential relationships and ignores the less essential ones.
• It is more easily understood than the empirical (i.e., observed) situation, and hence permits the problem to be solved more readily with minimum time and effort.
5. It can be used again and again for similar problems or can be modified.
   

4) What is Business Statistics?
The main objective of Business Statistics is to make inferences (e.g., prediction, making decisions) about certain characteristics of a population based on information contained in a random sample from the entire population. The condition for randomness is essential to make sure the sample is representative of the population.
Business Statistics is the science of ‘good' decision making in the face of uncertainty and is used in many disciplines, such as financial analysis, econometrics, auditing, production and operations, and marketing research. It provides knowledge and skills to interpret and use statistical techniques in a variety of business applications.
Statistics is a science of making decisions with respect to the characteristics of a group of persons or objects on the basis of numerical information obtained from a randomly selected sample of the group. Statisticians refer to this numerical observation as realization of a random sample. However, notice that one cannot see a random sample. A random sample is only a sample of a finite outcomes of a random process.
At the planning stage of a statistical investigation, the question of sample size (n) is critical. For example, sample size for sampling from a finite population of size N, is set at: N½+1, rounded up to the nearest integer. Clearly, a larger sample provides more relevant information, and as a result a more accurate estimation and better statistical judgement regarding test of hypotheses.
Hypothesis testing is a procedure for reaching a probabilistic conclusive decision about a claimed value for a population’s parameter based on a sample. To reduce this uncertainty and having high confidence that statistical inferences are correct, a sample must give equal chance to each member of population to be selected which can be achieved by sampling randomly and relatively large sample size n.
While business statistics cannot replace the knowledge and experience of the decision maker, it is a valuable tool that the manager can employ to assist in the decision making process in order to reduce the inherent risk, measured by, e.g., the standard deviation .

5) Common Statistical Terminology with Applications
Population: A population is any entire collection of people, animals, plants or things on which we may collect data. It is the entire group of interest, which we wish to describe or about which we wish to draw conclusions. In the above figure the life of the light bulbs manufactured say by GE, is the concerned population.

Qualitative and Quantitative Variables: Any object or event, which can vary in successive observations either in quantity or quality is called a"variable." Variables are classified accordingly as quantitative or qualitative. A qualitative variable, unlike a quantitative variable does not vary in magnitude in successive observations. The values of quantitative and qualitative variables are called"Variates" and"Attributes", respectively.
Variable: A characteristic or phenomenon, which may take different values, such as weight, gender since they are different from individual to individual.
Randomness: Randomness means unpredictability. The fascinating fact about inferential statistics is that, although each random observation may not be predictable when taken alone, collectively they follow a predictable pattern called its distribution function. For example, it is a fact that the distribution of a sample average follows a normal distribution for sample size over 30. In other words, an extreme value of the sample mean is less likely than an extreme value of a few raw data.

Sample: A subset of a population or universe.
An Experiment: An experiment is a process whose outcome is not known in advance with certainty.

Statistical Experiment: An experiment in general is an operation in which one chooses the values of some variables and measures the values of other variables, as in physics. A statistical experiment, in contrast is an operation in which one take a random sample from a population and infers the values of some variables. For example, in a survey, we"survey" i.e."look at" the situation without aiming to change it, such as in a survey of political opinions. A random sample from the relevant population provides information about the voting intentions.
Design of experiments is a key tool for increasing the rate of acquiring new knowledge. Knowledge in turn can be used to gain competitive advantage, shorten the product development cycle, and produce new products and processes which will meet and exceed your customer's expectations.

Primary data and Secondary data sets: If the data are from a planned experiment relevant to the objective(s) of the statistical investigation, collected by the analyst, it is called a Primary Data set. However, if some condensed records are given to the analyst, it is called a Secondary Data set.
Random Variable: A random variable is a real function (yes, it is called" variable", but in reality it is a function) that assigns a numerical value to each simple event. For example, in sampling for quality control an item could be defective or non-defective, therefore, one may assign X=1, and X = 0 for a defective and non-defective item, respectively. You may assign any other two distinct real numbers, as you wish; however, non-negative integer random variables are easy to work with. Random variables are needed since one cannot do arithmetic operations on words; the random variable enables us to compute statistics, such as average and variance. Any random variable has a distribution of probabilities associated with it.

Probability: Probability (i.e., probing for the unknown) is the tool used for anticipating what the distribution of data should look like under a given model. Random phenomena are not haphazard: they display an order that emerges only in the long run and is described by a distribution. The mathematical description of variation is central to statistics. The probability required for statistical inference is not primarily axiomatic or combinatorial, but is oriented toward describing data distributions.

Sampling Unit: A unit is a person, animal, plant or thing which is actually studied by a researcher; the basic objects upon which the study or experiment is executed. For example, a person; a sample of soil; a pot of seedlings; a zip code area; a doctor's practice.

Parameter: A parameter is an unknown value, and therefore it has to be estimated. Parameters are used to represent a certain population characteristic. For example, the population mean m is a parameter that is often used to indicate the average value of a quantity.
Statistic: A statistic is a quantity that is calculated from a sample of data. It is used to give information about unknown values in the corresponding population. For example, the average of the data in a sample is used to give information about the overall average in the population from which that sample was drawn.
Descriptive Statistics: The numerical statistical data should be presented clearly, concisely, and in such a way that the decision maker can quickly obtain the essential characteristics of the data in order to incorporate them into decision process.
The principal descriptive quantity derived from sample data is the mean (), which is the arithmetic average of the sample data. It serves as the most reliable single measure of the value of a typical member of the sample. If the sample contains a few values that are so large or so small that they have an exaggerated effect on the value of the mean, the sample is more accurately represented by the median -- the value where half the sample values fall below and half above.
Inferential Statistics: Inferential statistics is concerned with making inferences from samples about the populations from which they have been drawn. In other words, if we find a difference between two samples, we would like to know, is this a"real" difference (i.e., is it present in the population) or just a"chance" difference (i.e. it could just be the result of random sampling error). That's what tests of statistical significance are all about. Any inferred conclusion from a sample data to the population from which the sample is drawn must be expressed in a probabilistic term. Probability is the language and a measuring tool for uncertainty in our statistical conclusions.
Statistical Inference: Statistical inference refers to extending your knowledge obtained from a random sample from the entire population to the whole population. This is known in mathematics as Inductive Reasoning, that is, knowledge of the whole from a particular. Its main application is in hypotheses testing about a given population. Statistical inference guides the selection of appropriate statistical models. Models and data interact in statistical work. Inference from data can be thought of as the process of selecting a reasonable model, including a statement in probability language of how confident one can be about the selection.

Normal Distribution Condition: The normal or Gaussian distribution is a continuous symmetric distribution that follows the familiar bell-shaped curve. One of its nice features is that, the mean and variance uniquely and independently determines the distribution. It has been noted empirically that many measurement variables have distributions that are at least approximately normal. Even when a distribution is non-normal, the distribution of the mean of many independent observations from the same distribution becomes arbitrarily close to a normal distribution, as the number of observations grows large. Many frequently used statistical tests make the condition that the data come from a normal distribution.
Estimation and Hypothesis Testing:Inference in statistics are of two types. The first is estimation, which involves the determination, with a possible error due to sampling, of the unknown value of a population characteristic, such as the proportion having a specific attribute or the average value m of some numerical measurement. To express the accuracy of the estimates of population characteristics, one must also compute the standard errors of the estimates. The second type of inference is hypothesis testing. It involves the definitions of a hypothesis as one set of possible population values and an alternative, a different set. There are many statistical procedures for determining, on the basis of a sample, whether the true population characteristic belongs to the set of values in the hypothesis or the alternative.

6) Type of Data
Information can be collected in statistics using qualitative or quantitative data. Qualitative data, such as eye color of a group of individuals, is not computable by arithmetic relations. They are labels that advise in which category or class an individual, object, or process fall. They are called categorical variables.
Quantitative data sets consist of measures that take numerical values for which descriptions such as means and standard deviations are meaningful. They can be put into an order and further divided into two groups: discrete data or continuous data.
Discrete data are countable data and are collected by counting, for example, the number of defective items produced during a day's production.
Continuous data are collected by measuring and are expressed on a continuous scale. For example, measuring the height of a person.
Sampling Methods
Following are important methods in sampling:
Cluster sampling can be used whenever the population is homogeneous but can be partitioned. In many applications the partitioning is a result of physical distance. For instance, in the insurance industry, there are small"clusters" of employees in field offices scattered about the country. In such a case, a random sampling of employee work habits might not required travel to many of the"clusters" or field offices in order to get the data. Totally sampling each one of a small number of clusters chosen at random can eliminate much of the cost associated with the data requirements of management.
Stratified sampling can be used whenever the population can be partitioned into smaller sub-populations, each of which is homogeneous according to the particular characteristic of interest. If there are k sub-populations and we let Ni denote the size of sub-population i, let N denote the overall population size, and let n denote the sample size, then we select a stratified sample whenever we choose:

ni = n(Ni/N)
items at random from sub-population i, i = 1, 2, . . . ., k.
The estimates is:
s = S Wt. t, over t = 1, 2, ..L (strata), and t is SXit/nt.
Its variance is:
SW2t /(Nt-nt)S2t/[nt(Nt-1)]
Population total T is estimated by N. s; its variance is
SN2t(Nt-nt)S2t/[nt(Nt-1)].
Random sampling is probably the most popular sampling method used in decision making today. Many decisions are made, for instance, by choosing a number out of a hat or a numbered bead from a barrel, and both of these methods are attempts to achieve a random choice from a set of items. But true random sampling must be achieved with the aid of a computer or a random number table whose values are generated by computer random number generators.
A random sampling of size n is drawn from a population size N. The unbiased estimate for variance of is:
Var() = S2(1-n/N)/n,
where n/N is the sampling fraction. For sampling fraction less than 10% the finite population correction factor (N-n)/(N-1) is almost 1.
The total T is estimated by N ´ , its variance is N2Var().
For 0, 1, (binary) type variables, variation in estimated proportion p is:
S2 = p(1-p) ´ (1-n/N)/(n-1).
For ratio r = Sxi/Syi= / , the variation for r is:
[(N-n)(r2S2x + S2y -2 r Cov(x, y)]/[n(N-1)2].
Determination of sample sizes (n) with regard to binary data: Smallest integer greater than or equal to:
[t2 N p(1-p)] / [t2 p(1-p) + a2 (N-1)],
with N being the size of the total number of cases, n being the sample size, a the expected error, t being the value taken from the t-distribution corresponding to a certain confidence interval, and p being the probability of an event.
Cross-Sectional Sampling:Cross-Sectional study the observation of a defined population at a single point in time or time interval. Exposure and outcome are determined simultaneously.

7) Statistical Summaries
Mean: The arithmetic mean (or the average, simple mean) is computed by summing all numbers in an array of numbers (xi) and then dividing by the number of observations (n) in the array.
Mean = = S Xi /n,     the sum is over all i's.
The mean uses all of the observations, and each observation affects the mean. Even though the mean is sensitive to extreme values; i.e., extremely large or small data can cause the mean to be pulled toward the extreme data; it is still the most widely used measure of location. This is due to the fact that the mean has valuable mathematical properties that make it convenient for use with inferential statistical analysis. For example, the sum of the deviations of the numbers in a set of data from the mean is zero, and the sum of the squared deviations of the numbers in a set of data from the mean is the minimum value.
Weighted Mean: In some cases, the data in the sample or population should not be weighted equally, rather each value should be weighted according to its importance.
Median: The median is the middle value in an ordered array of observations. If there is an even number of observations in the array, the median is the average of the two middle numbers. If there is an odd number of data in the array, the median is the middle number.
Mode: The mode is the most frequently occurring value in a set of observations. Why use the mode? The classic example is the shirt/shoe manufacturer who wants to decide what sizes to introduce. Data may have two modes. In this case, we say the data are bimodal, and sets of observations with more than two modes are referred to as multimodal. Note that the mode is not a helpful measure of location, because there can be more than one mode or even no mode.
When the mean and the median are known, it is possible to estimate the mode for the unimodal distribution using the other two averages as follows:
Mode » 3(median) - 2(mean)

The Geometric Mean: The geometric mean (G) of n non-negative numerical values is the nth root of the product of the n values.
If some values are very large in magnitude and others are small, then the geometric mean is a better representative of the data than the simple average. In a"geometric series", the most meaningful average is the geometric mean (G). The arithmetic mean is very biased toward the larger numbers in the series.
The Harmonic Mean:The harmonic mean (H) is another specialized average, which is useful in averaging variables expressed as rate per unit of time, such as mileage per hour, number of units produced per day. The harmonic mean (H) of n non-zero numerical values x(i) is: H = n/[S (1/x(i)].
Range: The range of a set of observations is the absolute value of the difference between the largest and smallest values in the data set. It measures the size of the smallest contiguous interval of real numbers that encompasses all of the data values. It is not useful when extreme values are present. It is based solely on two values, not on the entire data set. In addition, it cannot be defined for open-ended distributions such as Normal distribution.
Notice that, when dealing with discrete random observations, some authors define the range as:
Range = Largest value - Smallest value + 1.
Quartiles: When we order the data, for example in ascending order, we may divide the data into quarters, Q1…Q4, known as quartiles. The first Quartile (Q1) is that value where 25% of the values are smaller and 75% are larger. The second Quartile (Q2) is that value where 50% of the values are smaller and 50% are larger. The third Quartile (Q3) is that value where 75% of the values are smaller and 25% are larger.
Percentiles: Percentiles have a similar concept and therefore, are related; e.g., the 25th percentile corresponds to the first quartile Q1, etc. The advantage of percentiles is that they may be subdivided into 100 parts. The percentiles and quartiles are most conveniently read from a cumulative distribution function.
Interquartiles Range: The interquartile range (IQR) describes the extent for which the middle 50% of the observations scattered or dispersed. It is the distance between the first and the third quartiles:
IQR = Q3 - Q1,
which is twice the Quartile Deviation. For data that are skewed, the relative dispersion, similar to the coefficient of variation (C.V.) is given (provided the denominator is not zero) by the Coefficient of Quartile Variation:
CQV = (Q3-Q1) / (Q3 + Q1).
Mean Absolute Deviation (MAD): A simple measure of variability is the mean absolute deviation:
MAD = S |(xi - )| / n.
The mean absolute deviation is widely used as a performance measure to assess the quality of the modeling, such forecasting techniques. However, MAD does not lend itself to further use in making inference; moreover, even in the error analysis studies, the variance is preferred since variances of independent (i.e., uncorrelated) errors are additive; however MAD does not have such a nice feature.
Variance: An important measure of variability is variance. Variance is the average of the squared deviations of each observation in the set from the arithmetic mean of all of the observations.
Variance = S (xi - ) 2 / (n - 1),     where n is at least 2.
Standard Deviation: Both variance and standard deviation provide the same information; one can always be obtained from the other. In other words, the process of computing a standard deviation always involves computing a variance. Since standard deviation is the square root of the variance, it is always expressed in the same units as the raw data:
Standard Deviation = S = (Variance) ½
The Mean Square Error (MSE) of an estimate is the variance of the estimate plus the square of its bias; therefore, if an estimate is unbiased, then its MSE is equal to its variance, as it is the case in the ANOVA table.
Coefficient of Variation: Coefficient of Variation (CV) is the absolute relative deviation with respect to size , provided is not zero, expressed in percentage:
CV =100 |S/| %
CV is independent of the unit of measurement. In estimation of a parameter, when its CV is less than 10%, the estimate is assumed acceptable. The inverse of CV; namely, 1/CV is called the Signal-to-noise Ratio.
Variation Ratio for Qualitative Data: Since the mode is the most frequently used measure of central tendency for qualitative variables, variability is measured with reference to the mode. The statistic that describes the variability of quantitative data is the Variation Ratio (VR):
VR = 1 - fm/n,
where fm is the frequency of the mode, and n is the total number of scores in the distribution.
Z Score: how many standard deviations a given point (i.e., observation) is above or below the mean. In other words, a Z score represents the number of standard deviations that an observation (x) is above or below the mean. The larger the Z value, the further away a value will be from the mean. Note that values beyond three standard deviations are very unlikely. Note that if a Z score is negative, the observation (x) is below the mean. If the Z score is positive, the observation (x) is above the mean. The Z score is found as:
Z = (x - ) / standard deviation of X
Z-Transformation: Applying the formula z = (X - m) / s will always produce a transformed variable with a mean of zero and a standard deviation of one. However, the shape of the distribution will not be affected by the transformation. If X is not normal, then the transformed distribution will not be normal either.
One of the nice features of the z-transformation is that the resulting distribution of the transformed data has an identical shape but with mean zero, and standard deviation equal to 1.
The z value refers to the critical value (a point on the horizontal axes) of the Normal (0, 1) density function, for a given area to the left of that z-value.
The z test refers to the procedures for testing the equality of mean (s) of one (or two) population(s).
The z score of a given observation x, in a sample of size n, is simply (x - average of the sample) divided by the standard deviation of the sample. One must be careful not to mistake z scores for the Standard Scores.
The z transformation of a set of observations of size n is simply (each observation - average of all observations) divided by the standard deviation among all observations. The aim is to produce a transformed data set with a mean of zero and a standard deviation of one. This makes the transformed set dimensionless and manageable with respect to its magnitudes. It is used also in comparing several data sets that have been measured using different scales of measurements.
Computation of Descriptive Statistics for Grouped Data: One of the most common ways to describe a single variable is with a frequency distribution. A histogram is a graphical presentation of an estimate for the frequency distribution of the population. Depending upon the particular variable, all of the data values may be represented, or you may group the values into categories first (e.g., by age). It would usually not be sensible to determine the frequencies for each value. Rather, the values are grouped into ranges, and the frequency is then determined.). Frequency distributions can be depicted in two ways: as a table or as a graph that is often referred to as a histogram or bar chart. The bar chart is often used to show the relationship between two categorical variables.
Grouped data is derived from raw data, and it consists of frequencies (counts of raw values) tabulated with the classes in which they occur. The Class Limits represent the largest (Upper) and lowest (Lower) values which the class will contain. The formulas for the descriptive statistic becomes much simpler for the grouped data, as shown below for Mean, Variance, Standard Deviation, respectively, where (f) is for the frequency of each class, and n is the total frequency:

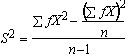
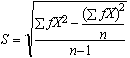
Shape of a Distribution Function:
The Skewness-Kurtosis Chart
Skewness: Skewness is a measure of the degree to which the sample population deviates from symmetry with the mean at the center.
Skewness = S (xi - ) 3 / [ (n - 1) S 3 ],    n is at least 2.
Skewness will take on a value of zero when the distribution is a symmetrical curve. A positive value indicates the observations are clustered more to the left of the mean with most of the extreme values to the right of the mean. A negative skewness indicates clustering to the right. In this case we have: Mean £ Median £ Mode. The reverse order holds for the observations with positive skewness.
Kurtosis: Kurtosis is a measure of the relative peakedness of the curve defined by the distribution of the observations.
Kurtosis = S (xi - ) 4 / [ (n - 1) S 4 ],     n is at least 2.
Standard normal distribution has kurtosis of +3. A kurtosis larger than 3 indicates the distribution is more peaked than the standard normal distribution.
Coefficient of Excess Kurtosis = Kurtosis - 3.
A value of less than 3 for kurtosis indicates that the distribution is flatter than the standard normal distribution.
It can be shown that,
Kurtosis - Skewness 2 is greater than or equal to 1, and
    Kurtosis is less than or equal to the sample size n.
These inequalities hold for any probability distribution having finite skewness and kurtosis.
In the Skewness-Kurtosis Chart, you notice two useful families of distributions, namely the beta and gamma families.

8) Probability, Chance, Likelihood, and Odds
The concept of probability occupies an important place in the decision-making process under uncertainty, whether the problem is one faced in business, in government, in the social sciences, or just in one's own everyday personal life. In very few decision-making situations is perfect information -- all the needed facts -- available. Most decisions are made in the face of uncertainty. Probability enters into the process by playing the role of a substitute for certainty - a substitute for complete knowledge.
Probability has an exact technical meaning -- well, in fact it has several, and there is still debate as to which term ought to be used. However, for most events for which probability is easily computed; e.g., rolling of a die, the probability of getting a four [::], almost all agree on the actual value (1/6), if not the philosophical interpretation. A probability is always a number between 0 and 1. Zero is not"quite" the same thing as impossibility. It is possible that"if" a coin were flipped infinitely many times, it would never show"tails", but the probability of an infinite run of heads is 0. One is not"quite" the same thing as certainty but close enough.
The word"chance" or"chances" is often used as an approximate synonym of "probability", either for variety or to save syllables. It would be better practice to leave"chance" for informal use, and say"probability" if that is what is meant. One occasionally sees"likely" and"likelihood"; however, these terms are used casually as synonyms for"probable" and"probability".
How to Assign Probabilities?
Probability is an instrument to measure the likelihood of the occurrence of an event. There are five major approaches of assigning probability: Classical Approach, Relative Frequency Approach, Subjective Approach, Anchoring, and the Delphi Technique:

1. Classical Approach: Classical probability is predicated on the condition that the outcomes of an experiment are equally likely to happen. The classical probability utilizes the idea that the lack of knowledge implies that all possibilities are equally likely. The classical probability is applied when the events have the same chance of occurring (called equally likely events), and the sets of events are mutually exclusive and collectively exhaustive. The classical probability is defined as:

P(X) = Number of favorable outcomes / Total number of possible outcomes

2. Relative Frequency Approach: Relative probability is based on accumulated historical or experimental data. Frequency-based probability is defined as:

P(X) = Number of times an event occurred / Total number of opportunities for the event to occur.
Note that relative probability is based on the ideas that what has happened in the past will hold.

3. Subjective Approach: The subjective probability is based on personal judgment and experience. For example, medical doctors sometimes assign subjective probability to the length of life expectancy for a person who has cancer.
4. Anchoring: is the practice of assigning a value obtained from a prior experience and adjusting the value in consideration of current expectations or circumstances
5. The Delphi Technique: It consists of a series of questionnaires. Each series is one"round". The responses from the first"round" are gathered and become the basis for the questions and feedback of the second"round". The process is usually repeated for a predetermined number of"rounds" or until the responses are such that a pattern is observed. This process allows expert opinion to be circulated to all members of the group and eliminates the bandwagon effect of majority opinion.

General Computational Probability Rules

1. Addition: When two or more events will happen at the same time, and the events are not mutually exclusive, then:

P (X or Y) = P (X) + P (Y) - P (X and Y)
Notice that, the equation P (X or Y) = P (X) + P (Y) - P (X and Y), contains especial events: An event (X and Y) which is the intersection of set/events X and Y, and another event (X or Y) which is the union (i.e., either/or) of sets X and Y. Although this is very simple, it says relatively little about how event X influences event Y and vice versa. If P (X and Y) is 0, indicating that events X and Y do not intersect (i.e., they are mutually exclusive), then we have P (X or Y) = P (X) + P (Y). On the other hand if P (X and Y) is not 0, then there are interactions between the two events X and Y. Usually it could be a physical interaction between them. This makes the relationship P (X or Y) = P (X) + P (Y) - P (X and Y) nonlinear because the P(X and Y) term is subtracted from which influences the result.
The above rule is known also as the Inclusion-Exclusion Formula. It can be extended to more than two events. For example, for three events A, B, and C, it becomes:
P(A or B or C) =
P(A) + P(B) + P(C) - P(A and B) - P(A and C) - P(B and C) + P(A and B and C)

2. Special Case of Addition: When two or more events will happen at the same time, and the events are mutually exclusive, then:

P(X or Y) = P(X) + P(Y)

3. General Multiplication Rule: When two or more events will happen at the same time, and the events are dependent, then the general rule of multiplicative rule is used to find the joint probability:

P(X and Y) = P(Y) ´ P(X|Y),
where P(X|Y) is a conditional probability.

4. Special Case of Multiplicative Rule: When two or more events will happen at the same time, and the events are independent, then the special rule of multiplication rule is used to find the joint probability:

P(X and Y) = P(X) ´ P(Y)

5. Conditional Probability: A conditional probability is denoted by P(X|Y). This phrase is read: the probability that X will occur given that Y is known to have occurred.

Conditional probabilities are based on knowledge of one of the variables. The conditional probability of an event, such as X, occurring given that another event, such as Y, has occurred is expressed as:
P(X|Y) = P(X and Y) ¸ P(Y),
provided P(Y) is not zero. Note that when using the conditional rule of probability, you always divide the joint probability by the probability of the event after the word given. Thus, to get P(X given Y), you divide the joint probability of X and Y by the unconditional probability of Y. In other words, the above equation is used to find the conditional probability for any two dependent events.
The simplest version of the Bayes' Theorem is:
P(X|Y) = P(Y|X) ´ P(X) ¸ P(Y)
If two events, such as X and Y, are independent then:
P(X|Y) = P(X),

and
P(Y|X) = P(Y)
 

9) Estimation
To estimate means to esteem (to give value to). An estimator is any quantity calculated from the sample data which is used to give information about an unknown quantity in the population. For example, the sample mean is an estimator of the population mean m.
Results of estimation can be expressed as a single value; known as a point estimate, or a range of values, referred to as a confidence interval. Whenever we use point estimation, we calculate the margin of error associated with that point estimation.
Estimators of population parameters are sometimes distinguished from the true value by using the symbol 'hat'. For example, true population standard deviation s is estimated from a sample population standard deviation.
Again, the usual estimator of the population mean is = Sxi / n, where n is the size of the sample and x1, x2, x3,.......,xn are the values of the sample. If the value of the estimator in a particular sample is found to be 5, then 5 is the estimate of the population mean µ.
Estimations with Confidence
In practice, a confidence interval is used to express the uncertainty in a quantity being estimated. There is uncertainty because inferences are based on a random sample of finite size from the entire population or process of interest. To judge the statistical procedure we can ask what would happen if we were to repeat the same study, over and over, getting different data (and thus different confidence intervals) each time.
Let's say you compute a 95% confidence interval for a mean m . The way to interpret this is to imagine an infinite number of samples from the same population, at leat 95% of the computed intervals will contain the population mean m , and at most 5% will not. However, it is wrong to state,"I am 95% confident that the population mean m falls within the interval."
Again, the usual definition of a 95% confidence interval is an interval constructed by a process such that the interval will contain the true value at least 95% of the time. This means that"95%" is a property of the process, not the interval.
Is the probability of occurrence of the population mean greater in the confidence interval (CI) center and lowest at the boundaries? Does the probability of occurrence of the population mean in a confidence interval vary in a measurable way from the center to the boundaries? In a general sense, normality condition is assumed, and then the interval between CI limits is represented by a bell shaped t distribution. The expectation (E) of another value is highest at the calculated mean value, and decreases as the values approach the CI limits.

Sample Size Determination
At the planning stage of a statistical investigation, the question of sample size (n) is critical. This is an important question therefore it should not be taken lightly. To take a larger sample than is needed to achieve the desired results is wasteful of resources, whereas very small samples often lead to what are no practical use of making good decisions. The main objective is to obtain both a desirable accuracy and a desirable confidence level with minimum cost.
The confidence level of conclusions drawn from a set of data depends on the size of the data set. The larger the sample, the higher is the associated confidence. However, larger samples also require more effort and resources. Thus, your goal must be to find the smallest sample size that will provide the desirable confidence.
For an item scored 0 or 1, for no or yes, the standard error (SE) of the estimated proportion p, based on your random sample observations, is given by:
SE = [p(1-p)/n]1/2
where p is the proportion obtaining a score of 1, and n is the sample size. This SE is the standard deviation of the range of possible estimate values.
The SE is at its maximum when p = 0.5, therefore the worst case scenario occurs when 50% are yes, and 50% are no.
Managing the Producer's or the Consumer's Risk
The logic behind a statistical test of hypothesis is similar to the following logic. Draw two lines on a paper and determine whether they are of different lengths. You compare them and say,"Well, certainly they are not equal. Therefore they must be of different lengths. By rejecting equality, that is, the null hypothesis, you assert that there is a difference.
The power of a statistical test is best explained by the overview of the Type I and Type II errors. The following matrix shows the basic representation of these errors.

The Type-I and Type-II Errors
As indicated in the above matrix a Type-I error occurs when, based on your data, you reject the null hypothesis when in fact it is true. The probability of a type-I error is the level of significance of the test of hypothesis and is denoted by a .
Type-I error is often called the producer's risk that consumers reject a good product or service indicated by the null hypothesis. That is, a producer introduces a good product, in doing so, he or she take a risk that consumer will reject it.
A type II error occurs when you do not reject the null hypothesis when it is in fact false. The probability of a type-II error is denoted by b . The quantity 1 - b is known as the Power of a Test. A Type-II error can be evaluated for any specific alternative hypotheses stated in the form"Not Equal to" as a competing hypothesis.
Type-II error is often called the consumer's risk for not rejecting possibly a worthless product or service indicated by the null hypothesis.
The following example highlights this concept. A electronics firm, Big Z, manufactures and sells a component part to a radio manufacturer, Big Y. Big Z consistently maintain a component part failure rate of 10% per 1000 parts produced. Here Big Z is the producer and Big Y is the consumer. Big Y, for reasons of practicality, will test sample of 10 parts out of lots of 1000. Big Y will adopt one of two rules regarding lot acceptance:

• Rule 1: Accept lots with one or fewer defectives; therefore, a lot has either 0 defective or 1 defective.
• Rule 2: Accept lots with two or fewer defectives; therefore, a lot has either 0,1, or 2 defective(s).

On the basis of the binomial distribution, the P(0 or 1) is 0.7367. This means that, with a defective rate of 0.10, the Big Y will accept 74% of tested lots and will reject 26% of the lots even though they are good lots. The 26% is the producer's risk or the a level. This a level is analogous to a Type I error -- rejecting a true null. Or, in other words, rejecting a good lot. In this example, for illustration purposes, the lot represents a null hypothesis. The rejected lot goes back to the producer; hence, producer's risk. If Big Y is to take rule 2, then the producer's risk decreases. The P(0 or, or 1, or 2) is 0.9298 therefore, Big Y will accept 93% of all tested lots, and 7% will be rejected, even though the lot is acceptable. The primary reason for this is that, although the probability of defective is 0.10, the Big Y through rule 2 allows for a higher defective acceptance rate. Big Y increases its own risk (consumer's risk), as stated previously.

Making Good Decision: Given that there is a relevant profit (which could be negative) for the outcome of your decision, and a prior probability (before testing) for the null hypothesis to be true, the objective is to make a good decision. Let us denote the profits for each cell in the decision table as $a, $b, $c and $d (column-wise), respectively. The expectation of profit is [aa + (1-a)b], and + [(1-b)c + bd], depending whether the null is true.

Now having a prior (i.e., before testing) subjective probability of p that the null is true, then the expected profit of your decision is:
Net Profit = [aa + (1-a)b]p + [(1-b)c + bd](1-p) - Sampling cost
A good decision makes this profit as large as possible. To this end, we must suitably choose the sample size and all other factors in the above profit function.
Note that, since we are using a subjective probability expressing the strength of belief assessment of the truthfulness of the null hypothesis, it is called a Bayesian Approach to statistical decision making, which is a standard approach in decision theory.

10) Regression Modeling and Analysis
Many problems in analyzing data involve describing how variables are related. The simplest of all models describing the relationship between two variables is a linear, or straight-line, model. Linear regression is always linear in the coefficients being estimated, not necessarily linear in the variables.
The simplest method of drawing a linear model is to"eye-ball" a line through the data on a plot, but a more elegant, and conventional method is that of least squares, which finds the line minimizing the sum of the vertical distances between observed points and the fitted line. Realize that fitting the"best" line by eye is difficult, especially when there is much residual variability in the data.
Know that there is a simple connection between the numerical coefficients in the regression equation and the slope and intercept of the regression line.
Again, the regression line is a group of estimates for the variable plotted on the Y-axis. It has a form of y = b + mx, where m is the slope of the line. The slope is the rise over run. If a line goes up 2 for each 1 it goes over, then its slope is 2.
The regression line goes through a point with coordinates of (mean of x values, mean of y values), known as the mean-mean point.
If you plug each x in the regression equation, then you obtain a predicted value for y. The difference between the predicted y and the observed y is called a residual, or an error term. Some errors are positive and some are negative. The sum of squares of the errors plus the sum of squares of the estimates add up to the sum of squares of Y:

Partitioning the Three Sum of Squares

The regression line is the line that minimizes the variance of the errors. The mean error is zero; so, this means that it minimizes the sum of the squares errors.
The reason for finding the best fitting line is so that you can make a reasonable prediction of what y will be if x is known (not vise-versa).
r2 is the variance of the estimates divided by the variance of Y. r is the size of the slope of the regression line, in terms of standard deviations. In other words, it is the slope of the regression line if we use the standardized X and Y. It is how many standard deviations of Y you would go up, when you go one standard deviation of X to the right.
Coefficient of Determination: Another measure of the closeness of the points to the regression line is the Coefficient of Determination:
r2 = SSyhat yhat / SSyy
which is the amount of the squared deviation in Y, that is explained by the points on the least squares regression line.
Standardized Regression Analysis: The scale of measurements used to measure X and Y has major impact on the regression equation and correlation coefficient. This impact is more drastic comparing two regression equations having different scales of measurement. To overcome these drawbacks, one must standardize both X and Y prior to constructing the regression and interpreting the results. In such a model, the slope is equal to the correlation coefficient r. Notice that the derivative of function Y with respect to dependent variable X is the correlation coefficient. Therefore, there is a nice similarity in the meaning of r in statistics and the derivative from calculus, in that its sign and its magnitude reveal the increasing/decreasing and the rate of change, as the derivative of a function do.
In the usual regression modeling the estimated slope and intercept are correlated; therefore, any error in estimating the slope influences the estimate of the intercept. One of the main advantages of using the standardized data is that the intercept is always equal to zero.
Regression when both X and Y are random: Simple linear least-squares regression has among its conditions that the data for the independent (X) variables are known without error. In fact, the estimated results are conditioned on whatever errors happened to be present in the independent data sets. When the X-data have an error associated with them the result is to bias the slope downwards. A procedure known as Deming regression can handle this problem quite well. Biased slope estimates (due to error in X) can be avoided using Deming regression.
If X and Y are random variables, then the correlation coefficient R is often referred to as the Coefficient of Reliability.
The Relationship Between Slope and Correlation Coefficient: By a little bit of algebraic manipulation, one can show that the coefficient of correlation is related to the slope of the two regression lines: Y on X, and X on Y, denoted by m yx and mxy, respectively:
R2 = m yx . mxy
Lines of regression through the origin: Often the conditions of a practical problem require that the regression line go through the origin (x = 0, y = 0). In such a case, the regression line has one parameter only, which is its slope:
m = S (xi ´ yi)/ Sxi2
Correlation, and Level of Significance
It is intuitive that with very few data points, a high correlation may not be statistically significant. You may see statements such as,"correlation is significant between x and y at the a = 0.005 level" and"correlation is significant at the a = 0.05 level." The question is: how do you determine these numbers?
Using the simple correlation r, the formula for F-statistic is:
F= (n-2) r2 / (1-r2),     where n is at least 2.
As you see, F statistic is monotonic function with respect to both: r2, and the sample size n.
Notice that the test for the statistical significance of a correlation coefficient requires that the two variables be distributed as a bivariate normal.

11) Index Numbers and Ratios
When facing a lack of a unit of measure, we often use indicators as surrogates for direct measurement. For example, the height of a column of mercury is a familiar indicator of temperature. No one presumes that the height of mercury column constitutes temperature in quite the same sense that length constitutes the number of centimeters from end to end. However, the height of a column of mercury is a dependable correlate of temperature and thus serves as a useful measure of it. Therefore, and indicator is an accessible and dependable correlate of a dimension of interest; that correlate is used as a measure of that dimension because direct measurement of the dimension is not possible or practical. In like manner index numbers serve as surrogate for actual data.
The primary purposes of an index number are to provide a value useful for comparing magnitudes of aggregates of related variables to each other, and to measure the changes in these magnitudes over time. Consequently, many different index numbers have been developed for special use. There are a number of particularly well-known ones, some of which are announced on public media every day. Government agencies often report time series data in the form of index numbers. For example, the consumer price index is an important economic indicator. Therefore, it is useful to understand how index numbers are constructed and how to interpret them. These index numbers are developed usually starting with base 100 that indicates a change in magnitude relative to its value at a specified point in time.
Consumer Price Index
The simplest and widely used measure of inflation is the Consumer Price Index (CPI). To compute the price index, the cost of the market basket in any period is divided by the cost of the market basket in the base period, and the result is multiplied by 100.
If you want to forecast the economic future, you can do so without knowing anything about how the economy works. Further, your forecasts may turn out to be as good as those of professional economists. The key to your success will be the Leading Indicators, an index of items that generally swing up or down before the economy as a whole does.

we found that using period 1 quantity, the price index in period 2 is
($4.39/$4.25) x 100 = 103.29
Using period 2 quantities, the price index in period 2 is
($4.31/$4.35) x 100 = 99.08
A better price index could be found by taking the geometric mean of the two. To find the geometric mean, multiply the two together and then take the square root. The result is called a Fisher Index.
In USA, since January 1999, the geometric mean formula has been used to calculate most basic indexes within the Comsumer Price Indeces (CPI); in other words, the prices within most item categories (e.g., apples) are averaged using a geometric mean formula. This improvement moves the CPI somewhat closer to a cost-of-living measure, as the geometric mean formula allows for a modest amount of consumer substitution as relative prices within item categories change.
Notice that, since the geometric mean formula is used only to average prices within item categories, it does not account for consumer substitution taking place between item categories. For example, if the price of pork increases compared to those of other meats, shoppers might shift their purchases away from pork to beef, poultry, or fish. The CPI formula does not reflect this type of consumer response to changing relative prices.
Ratio Index Numbers
The following provides the computational procedures with applications for some Index numbers, including the Ratio Index, and Composite Index numbers.
Suppose we are interested in the labor utilization of two manufacturing plants A and B with the unit outputs and man/hours, as shown in the following table, together with the national standard over the last three months:

The labor utilization for the Plant A in the first month is:
LA,1 = [(200000/283)] / [(600000/4000)] = 4.69
Similarly,
LB,3 = 53.59/50 = 1.07.
Upon computing the labor utilization for both plants for each month, one can present the results by graphing the labor utilization over time for comparative studies.
Composite Index Numbers
Consider the total labor, and material cost for two consecutive years for an industrial plant, as shown in the following table:

From the information given in the above table, the index for the two consecutive years are 500/500 = 1, and 560/500 = 1.12, respectively.
Labor Force Unemployment Index
Is a given city an economically depressed area? The degree of unemployment among labor (L) force is considered to be a proper indicator of economic depression. To construct the unemployment index, each person is classified both with respect to membership in the labor force and the degree of unemployment in fractional value, ranging from 0 to 1. The fraction that indicates the portion of labor that is idle is:
L = S[UiPi] / SPi,    the sums are over all i = 1, 2,…, n.
where Pi is the proportion of a full workweek for each resident of the area held or sought employment and n is the total number of residents in the area. Ui is the proportion of Pi for which each resident of the area unemployed. For example, a person seeking two days of work per week (5 days) and employed for only one-half day would be identified with Pi = 2/5 = 0.4, and Ui = 1.5/2 = 0.75. The resulting multiplication UiPi = 0.3 would be the portion of a full workweek for which the person was unemployed.
Now the question is What value of L constitutes an economic depressed area. The answer belongs to the decision-maker to decide.

Bibliography
D

Daston L. (1988), Classical Probability in the Enlightenment, Princeton University Press.
G
Gillies D. (2000), Philosophical Theories of Probability, Routledge.
H
Hacking I. (1975), The Emergence of Probability, Cambridge University Press, London.

Hald A. (2003), A History of Probability and Statistics and Their Applications before 1750, Wiley.
L
Lapin L. (1987), Statistics for Modern Business Decisions, Harcourt Brace Jovanovich.

P
Pratt J., H. Raiffa, and R. Schlaifer (1994), Introduction to Statistical Decision Theory, The MIT Press.
T
Tankard J. (1984), The Statistical Pioneers, Schenkman Books, New York.